Quad#

Represents a four-sided mathematical shape (also called “quadrilateral” or “tetragon”) in the plane, defined as a sequence of four Point objects ul, ur, ll, lr (conveniently called upper left, upper right, lower left, lower right).

Quads can be obtained as results of text search methods (Page.search_for()), and they are used to define text marker annotations (see e.g. Page.add_squiggly_annot() and friends), and in several draw methods (like Page.draw_quad() / Shape.draw_quad(), Page.draw_oval()/ Shape.draw_quad()).

Note

If the corners of a rectangle are transformed with a rotation, scale or translation Matrix, then the resulting quad is rectangular (= congruent to a rectangle), i.e. all of its corners again enclose angles of 90 degrees. Property Quad.is_rectangular checks whether a quad can be thought of being the result of such an operation.
This is not true for all matrices: e.g. shear matrices produce parallelograms, and non-invertible matrices deliver “degenerate” tetragons like triangles or lines.
Attribute Quad.rect obtains the enveloping rectangle. Vice versa, rectangles now have attributes Rect.quad, resp. IRect.quad to obtain their respective tetragon versions.

Methods / Attributes	Short Description
`Quad.transform()`	transform with a matrix
`Quad.morph()`	transform with a point and matrix
`Quad.ul`	upper left point
`Quad.ur`	upper right point
`Quad.ll`	lower left point
`Quad.lr`	lower right point
`Quad.is_convex`	true if quad is a convex set
`Quad.is_empty`	true if quad is an empty set
`Quad.is_rectangular`	true if quad is congruent to a rectangle
`Quad.rect`	smallest containing Rect
`Quad.width`	the longest width value
`Quad.height`	the longest height value

Class API

class Quad#

__init__(self)#

__init__(self, ul, ur, ll, lr)#

__init__(self, quad)#

__init__(self, sequence)#

Overloaded constructors: “ul”, “ur”, “ll”, “lr” stand for point_like objects (the four corners), “sequence” is a Python sequence with four point_like objects.

If “quad” is specified, the constructor creates a new copy of it.

Without parameters, a quad consisting of 4 copies of Point(0, 0) is created.

transform(matrix)#

Modify the quadrilateral by transforming each of its corners with a matrix.

Parameters:: matrix (matrix_like) – the matrix.

morph(fixpoint, matrix)#

(New in version 1.17.0) “Morph” the quad with a matrix-like using a point-like as fixed point.

Parameters:

fixpoint (point_like) – the point.
matrix (matrix_like) – the matrix.

Returns:

a new quad (no operation if this is the infinite quad).

rect#

The smallest rectangle containing the quad, represented by the blue area in the following picture.

Type:: Rect

ul#

Upper left point.

Type:: Point

ur#

Upper right point.

Type:: Point

ll#

Lower left point.

Type:: Point

lr#

Lower right point.

Type:: Point

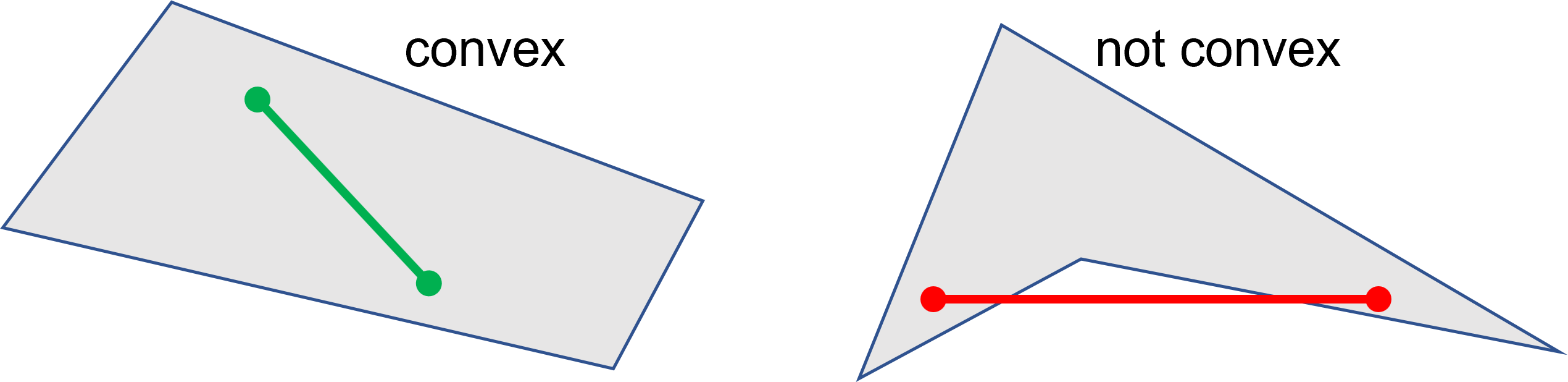
is_convex#

New in version 1.16.1

Checks if for any two points of the quad, all points on their connecting line also belong to the quad.

Type:: bool

is_empty#

True if enclosed area is zero, which means that at least three of the four corners are on the same line. If this is false, the quad may still be degenerate or not look like a tetragon at all (triangles, parallelograms, trapezoids, …).

Type:: bool

is_rectangular#

True if all corner angles are 90 degrees. This implies that the quad is convex and not empty.

Type:: bool

width#

The maximum length of the top and the bottom side.

Type:: float

height#

The maximum length of the left and the right side.

Type:: float

Remark#

This class adheres to the sequence protocol, so components can be dealt with via their indices, too. Also refer to Using Python Sequences as Arguments in PyMuPDF.

Algebra and Containment Checks#

Starting with v1.19.6, quads can be used in algebraic expressions like the other geometry object – the respective restrictions have been lifted. In particular, all the following combinations of containment checking are now possible:

{Point | IRect | Rect | Quad} in {IRect | Rect | Quad}

Please note the following interesting detail:

For a rectangle, only its top-left point belongs to it. Since v1.19.0, rectangles are defined to be “open”, such that its bottom and its right edge do not belong to it – including the respective corners. But for quads there exists no such notion like “openness”, so we have the following somewhat surprising implication:

>>> rect.br in rect
False
>>> # but:
>>> rect.br in rect.quad
True

Do you have any feedback on this page?

This software is provided AS-IS with no warranty, either express or implied. This software is distributed under license and may not be copied, modified or distributed except as expressly authorized under the terms of that license. Refer to licensing information at artifex.com or contact Artifex Software Inc., 39 Mesa Street, Suite 108A, San Francisco CA 94129, United States for further information.