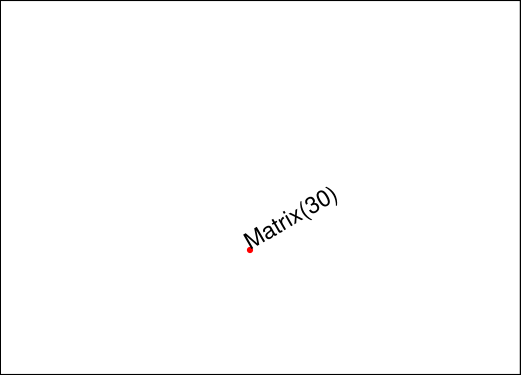Matrix#

Matrix is a row-major 3x3 matrix used by image transformations in MuPDF (which complies with the respective concepts laid down in the Adobe PDF References). With matrices you can manipulate the rendered image of a page in a variety of ways: (parts of) the page can be rotated, zoomed, flipped, sheared and shifted by setting some or all of just six float values.

Since all points or pixels live in a two-dimensional space, one column vector of that matrix is a constant unit vector, and only the remaining six elements are used for manipulations. These six elements are usually represented by [a, b, c, d, e, f]. Here is how they are positioned in the matrix:

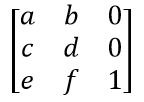
Please note:

the below methods are just convenience functions – everything they do, can also be achieved by directly manipulating the six numerical values

all manipulations can be combined – you can construct a matrix that rotates and shears and scales and shifts, etc. in one go. If you however choose to do this, do have a look at the remarks further down or at the Adobe PDF References.

Method / Attribute	Description
`Matrix.prerotate()`	perform a rotation
`Matrix.prescale()`	perform a scaling
`Matrix.preshear()`	perform a shearing (skewing)
`Matrix.pretranslate()`	perform a translation (shifting)
`Matrix.concat()`	perform a matrix multiplication
`Matrix.invert()`	calculate the inverted matrix
`Matrix.norm()`	the Euclidean norm
`Matrix.a`	zoom factor X direction
`Matrix.b`	shearing effect Y direction
`Matrix.c`	shearing effect X direction
`Matrix.d`	zoom factor Y direction
`Matrix.e`	horizontal shift
`Matrix.f`	vertical shift
`Matrix.is_rectilinear`	true if rect corners will remain rect corners

Class API

class Matrix#

__init__(self)#

__init__(self, zoom-x, zoom-y)#

__init__(self, shear-x, shear-y, 1)#

__init__(self, a, b, c, d, e, f)#

__init__(self, matrix)#

__init__(self, degree)#

__init__(self, sequence)#

Overloaded constructors.

Without parameters, the zero matrix Matrix(0.0, 0.0, 0.0, 0.0, 0.0, 0.0) will be created.

zoom-* and shear-* specify zoom or shear values (float) and create a zoom or shear matrix, respectively.

For “matrix” a new copy of another matrix will be made.

Float value “degree” specifies the creation of a rotation matrix which rotates anti-clockwise.

A “sequence” must be any Python sequence object with exactly 6 float entries (see Using Python Sequences as Arguments in PyMuPDF).

fitz.Matrix(1, 1) and fitz.Matrix(fitz.Identity) create modifiable versions of the Identity matrix, which looks like [1, 0, 0, 1, 0, 0].

norm()#

New in version 1.16.0

Return the Euclidean norm of the matrix as a vector.

prerotate(deg)#

Modify the matrix to perform a counter-clockwise rotation for positive deg degrees, else clockwise. The matrix elements of an identity matrix will change in the following way:

[1, 0, 0, 1, 0, 0] -> [cos(deg), sin(deg), -sin(deg), cos(deg), 0, 0].

Parameters:: deg (float) – The rotation angle in degrees (use conventional notation based on Pi = 180 degrees).

prescale(sx, sy)#

Modify the matrix to scale by the zoom factors sx and sy. Has effects on attributes a thru d only: [a, b, c, d, e, f] -> [a*sx, b*sx, c*sy, d*sy, e, f].

Parameters:

sx (float) – Zoom factor in X direction. For the effect see description of attribute a.
sy (float) – Zoom factor in Y direction. For the effect see description of attribute d.

preshear(sx, sy)#

Modify the matrix to perform a shearing, i.e. transformation of rectangles into parallelograms (rhomboids). Has effects on attributes a thru d only: [a, b, c, d, e, f] -> [c*sy, d*sy, a*sx, b*sx, e, f].

Parameters:

sx (float) – Shearing effect in X direction. See attribute c.
sy (float) – Shearing effect in Y direction. See attribute b.

pretranslate(tx, ty)#

Modify the matrix to perform a shifting / translation operation along the x and / or y axis. Has effects on attributes e and f only: [a, b, c, d, e, f] -> [a, b, c, d, tx*a + ty*c, tx*b + ty*d].

Parameters:

tx (float) – Translation effect in X direction. See attribute e.
ty (float) – Translation effect in Y direction. See attribute f.

concat(m1, m2)#

Calculate the matrix product m1 * m2 and store the result in the current matrix. Any of m1 or m2 may be the current matrix. Be aware that matrix multiplication is not commutative. So the sequence of m1, m2 is important.

Parameters:

m1 (Matrix) – First (left) matrix.
m2 (Matrix) – Second (right) matrix.

invert(m=None)#

Calculate the matrix inverse of m and store the result in the current matrix. Returns 1 if m is not invertible (“degenerate”). In this case the current matrix will not change. Returns 0 if m is invertible, and the current matrix is replaced with the inverted m.

Parameters:: m (Matrix) – Matrix to be inverted. If not provided, the current matrix will be used.
Return type:: int

a#

Scaling in X-direction (width). For example, a value of 0.5 performs a shrink of the width by a factor of 2. If a < 0, a left-right flip will (additionally) occur.

Type:: float

b#

Causes a shearing effect: each Point(x, y) will become Point(x, y - b*x). Therefore, horizontal lines will be “tilt”.

Type:: float

c#

Causes a shearing effect: each Point(x, y) will become Point(x - c*y, y). Therefore, vertical lines will be “tilt”.

Type:: float

d#

Scaling in Y-direction (height). For example, a value of 1.5 performs a stretch of the height by 50%. If d < 0, an up-down flip will (additionally) occur.

Type:: float

e#

Causes a horizontal shift effect: Each Point(x, y) will become Point(x + e, y). Positive (negative) values of e will shift right (left).

Type:: float

f#

Causes a vertical shift effect: Each Point(x, y) will become Point(x, y - f). Positive (negative) values of f will shift down (up).

Type:: float

is_rectilinear#

Rectilinear means that no shearing is present and that any rotations are integer multiples of 90 degrees. Usually this is used to confirm that (axis-aligned) rectangles before the transformation are still axis-aligned rectangles afterwards.

Type:: bool

Note

This class adheres to the Python sequence protocol, so components can be accessed via their index, too. Also refer to Using Python Sequences as Arguments in PyMuPDF.
Matrices can be used with arithmetic operators almost like ordinary numbers: they can be added, subtracted, multiplied or divided – see chapter Operator Algebra for Geometry Objects.
Matrix multiplication is not commutative – changing the sequence of the multiplicands will change the result in general. So it can quickly become unclear which result a transformation will yield.

Examples#

Here are examples that illustrate some of the achievable effects. All pictures show some text, inserted under control of some matrix and relative to a fixed reference point (the red dot).

The Identity matrix performs no operation.

The scaling matrix Matrix(2, 0.5) stretches by a factor of 2 in horizontal, and shrinks by factor 0.5 in vertical direction.

Attributes Matrix.e and Matrix.f shift horizontally and, respectively vertically. In the following 10 to the right and 20 down.

A negative Matrix.a causes a left-right flip.

A negative Matrix.d causes an up-down flip.

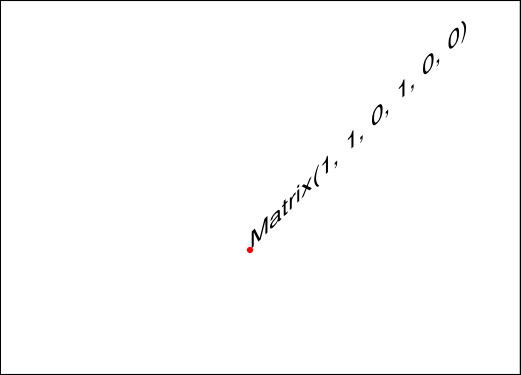
Attribute Matrix.b tilts upwards / downwards along the x-axis.

Attribute Matrix.c tilts left / right along the y-axis.

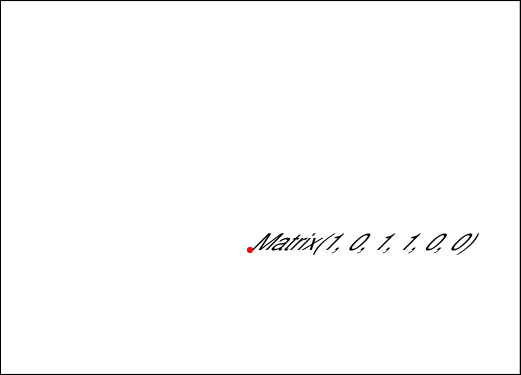
Matrix Matrix(beta) performs counterclockwise rotations for positive angles beta.

Do you have any feedback on this page?

This software is provided AS-IS with no warranty, either express or implied. This software is distributed under license and may not be copied, modified or distributed except as expressly authorized under the terms of that license. Refer to licensing information at artifex.com or contact Artifex Software Inc., 39 Mesa Street, Suite 108A, San Francisco CA 94129, United States for further information.