Appendix 3: Assorted Technical Information#
This section deals with various technical topics, that are not necessarily related to each other.
Image Transformation Matrix#
Starting with version 1.18.11, the image transformation matrix is returned by some methods for text and image extraction: Page.get_text() and Page.get_image_bbox().
The transformation matrix contains information about how an image was transformed to fit into the rectangle (its “boundary box” = “bbox”) on some document page. By inspecting the image’s bbox on the page and this matrix, one can determine for example, whether and how the image is displayed scaled or rotated on a page.
The relationship between image dimension and its bbox on a page is the following:
- Using the original image’s width and height,
define the image rectangle
imgrect = fitz.Rect(0, 0, width, height)define the “shrink matrix”
shrink = fitz.Matrix(1/width, 0, 0, 1/height, 0, 0).
Transforming the image rectangle with its shrink matrix, will result in the unit rectangle:
imgrect * shrink = fitz.Rect(0, 0, 1, 1).Using the image transformation matrix “transform”, the following steps will compute the bbox:
imgrect = fitz.Rect(0, 0, width, height) shrink = fitz.Matrix(1/width, 0, 0, 1/height, 0, 0) bbox = imgrect * shrink * transform
Inspecting the matrix product
shrink * transformwill reveal all information about what happened to the image rectangle to make it fit into the bbox on the page: rotation, scaling of its sides and translation of its origin. Let us look at an example:>>> imginfo = page.get_images()[0] # get an image item on a page >>> imginfo (5, 0, 439, 501, 8, 'DeviceRGB', '', 'fzImg0', 'DCTDecode') >>> #------------------------------------------------ >>> # define image shrink matrix and rectangle >>> #------------------------------------------------ >>> shrink = fitz.Matrix(1 / 439, 0, 0, 1 / 501, 0, 0) >>> imgrect = fitz.Rect(0, 0, 439, 501) >>> #------------------------------------------------ >>> # determine image bbox and transformation matrix: >>> #------------------------------------------------ >>> bbox, transform = page.get_image_bbox("fzImg0", transform=True) >>> #------------------------------------------------ >>> # confirm equality - permitting rounding errors >>> #------------------------------------------------ >>> bbox Rect(100.0, 112.37525939941406, 300.0, 287.624755859375) >>> imgrect * shrink * transform Rect(100.0, 112.375244140625, 300.0, 287.6247253417969) >>> #------------------------------------------------ >>> shrink * transform Matrix(0.0, -0.39920157194137573, 0.3992016017436981, 0.0, 100.0, 287.6247253417969) >>> #------------------------------------------------ >>> # the above shows: >>> # image sides are scaled by same factor ~0.4, >>> # and the image is rotated by 90 degrees clockwise >>> # compare this with fitz.Matrix(-90) * 0.4 >>> #------------------------------------------------
PDF Base 14 Fonts#
The following 14 builtin font names must be supported by every PDF viewer application. They are available as a dictionary, which maps their full names amd their abbreviations in lower case to the full font basename. Wherever a fontname must be provided in PyMuPDF, any key or value from the dictionary may be used:
In [2]: fitz.Base14_fontdict
Out[2]:
{'courier': 'Courier',
'courier-oblique': 'Courier-Oblique',
'courier-bold': 'Courier-Bold',
'courier-boldoblique': 'Courier-BoldOblique',
'helvetica': 'Helvetica',
'helvetica-oblique': 'Helvetica-Oblique',
'helvetica-bold': 'Helvetica-Bold',
'helvetica-boldoblique': 'Helvetica-BoldOblique',
'times-roman': 'Times-Roman',
'times-italic': 'Times-Italic',
'times-bold': 'Times-Bold',
'times-bolditalic': 'Times-BoldItalic',
'symbol': 'Symbol',
'zapfdingbats': 'ZapfDingbats',
'helv': 'Helvetica',
'heit': 'Helvetica-Oblique',
'hebo': 'Helvetica-Bold',
'hebi': 'Helvetica-BoldOblique',
'cour': 'Courier',
'coit': 'Courier-Oblique',
'cobo': 'Courier-Bold',
'cobi': 'Courier-BoldOblique',
'tiro': 'Times-Roman',
'tibo': 'Times-Bold',
'tiit': 'Times-Italic',
'tibi': 'Times-BoldItalic',
'symb': 'Symbol',
'zadb': 'ZapfDingbats'}
In contrast to their obligation, not all PDF viewers support these fonts correctly and completely – this is especially true for Symbol and ZapfDingbats. Also, the glyph (visual) images will be specific to every reader.
To see how these fonts can be used – including the CJK built-in fonts – look at the table in Page.insert_font().
Adobe PDF References#
This PDF Reference manual published by Adobe is frequently quoted throughout this documentation. It can be viewed and downloaded from here.
Note
For a long time, an older version was also available under this link. It seems to be taken off of the web site in October 2021. Earlier (pre 1.19.*) versions of the PyMuPDF documentation used to refer to this document. We have undertaken an effort to replace referrals to the current specification above.
Using Python Sequences as Arguments in PyMuPDF#
When PyMuPDF objects and methods require a Python list of numerical values, other Python sequence types are also allowed. Python classes are said to implement the sequence protocol, if they have a __getitem__() method.
This basically means, you can interchangeably use Python list or tuple or even array.array, numpy.array and bytearray types in these cases.
For example, specifying a sequence "s" in any of the following ways
s = [1, 2]– a lists = (1, 2)– a tuples = array.array("i", (1, 2))– an array.arrays = numpy.array((1, 2))– a numpy arrays = bytearray((1, 2))– a bytearray
will make it usable in the following example expressions:
fitz.Point(s)fitz.Point(x, y) + sdoc.select(s)
Similarly with all geometry objects Rect, IRect, Matrix and Point.
Because all PyMuPDF geometry classes themselves are special cases of sequences, they (with the exception of Quad – see below) can be freely used where numerical sequences can be used, e.g. as arguments for functions like list(), tuple(), array.array() or numpy.array(). Look at the following snippet to see this work.
>>> import fitz, array, numpy as np
>>> m = fitz.Matrix(1, 2, 3, 4, 5, 6)
>>>
>>> list(m)
[1.0, 2.0, 3.0, 4.0, 5.0, 6.0]
>>>
>>> tuple(m)
(1.0, 2.0, 3.0, 4.0, 5.0, 6.0)
>>>
>>> array.array("f", m)
array('f', [1.0, 2.0, 3.0, 4.0, 5.0, 6.0])
>>>
>>> np.array(m)
array([1., 2., 3., 4., 5., 6.])
Note
Quad is a Python sequence object as well and has a length of 4. Its items however are point_like – not numbers. Therefore, the above remarks do not apply.
Ensuring Consistency of Important Objects in PyMuPDF#
PyMuPDF is a Python binding for the C library MuPDF. While a lot of effort has been invested by MuPDF’s creators to approximate some sort of an object-oriented behavior, they certainly could not overcome basic shortcomings of the C language in that respect.
Python on the other hand implements the OO-model in a very clean way. The interface code between PyMuPDF and MuPDF consists of two basic files: fitz.py and fitz_wrap.c. They are created by the excellent SWIG tool for each new version.
When you use one of PyMuPDF’s objects or methods, this will result in execution of some code in fitz.py, which in turn will call some C code compiled with fitz_wrap.c.
Because SWIG goes a long way to keep the Python and the C level in sync, everything works fine, if a certain set of rules is being strictly followed. For example: never access a Page object, after you have closed (or deleted or set to None) the owning Document. Or, less obvious: never access a page or any of its children (links or annotations) after you have executed one of the document methods select(), delete_page(), insert_page() … and more.
But just no longer accessing invalidated objects is actually not enough: They should rather be actively deleted entirely, to also free C-level resources (meaning allocated memory).
The reason for these rules lies in the fact that there is a hierarchical 2-level one-to-many relationship between a document and its pages and also between a page and its links / annotations. To maintain a consistent situation, any of the above actions must lead to a complete reset – in Python and, synchronously, in C.
SWIG cannot know about this and consequently does not do it.
The required logic has therefore been built into PyMuPDF itself in the following way.
If a page “loses” its owning document or is being deleted itself, all of its currently existing annotations and links will be made unusable in Python, and their C-level counterparts will be deleted and deallocated.
If a document is closed (or deleted or set to None) or if its structure has changed, then similarly all currently existing pages and their children will be made unusable, and corresponding C-level deletions will take place. “Structure changes” include methods like select(), delePage(), insert_page(), insert_pdf() and so on: all of these will result in a cascade of object deletions.
The programmer will normally not realize any of this. If he, however, tries to access invalidated objects, exceptions will be raised.
Invalidated objects cannot be directly deleted as with Python statements like del page or page = None, etc. Instead, their __del__ method must be invoked.
All pages, links and annotations have the property parent, which points to the owning object. This is the property that can be checked on the application level: if obj.parent == None then the object’s parent is gone, and any reference to its properties or methods will raise an exception informing about this “orphaned” state.
A sample session:
>>> page = doc[n]
>>> annot = page.first_annot
>>> annot.type # everything works fine
[5, 'Circle']
>>> page = None # this turns 'annot' into an orphan
>>> annot.type
<... omitted lines ...>
RuntimeError: orphaned object: parent is None
>>>
>>> # same happens, if you do this:
>>> annot = doc[n].first_annot # deletes the page again immediately!
>>> annot.type # so, 'annot' is 'born' orphaned
<... omitted lines ...>
RuntimeError: orphaned object: parent is None
This shows the cascading effect:
>>> doc = fitz.open("some.pdf")
>>> page = doc[n]
>>> annot = page.first_annot
>>> page.rect
fitz.Rect(0.0, 0.0, 595.0, 842.0)
>>> annot.type
[5, 'Circle']
>>> del doc # or doc = None or doc.close()
>>> page.rect
<... omitted lines ...>
RuntimeError: orphaned object: parent is None
>>> annot.type
<... omitted lines ...>
RuntimeError: orphaned object: parent is None
Note
Objects outside the above relationship are not included in this mechanism. If you e.g. created a table of contents by toc = doc.get_toc(), and later close or change the document, then this cannot and does not change variable toc in any way. It is your responsibility to refresh such variables as required.
Design of Method Page.show_pdf_page()#
Purpose and Capabilities#
The method displays an image of a (“source”) page of another PDF document within a specified rectangle of the current (“containing”, “target”) page.
In contrast to
Page.insert_image(), this display is vector-based and hence remains accurate across zooming levels.Just like
Page.insert_image(), the size of the display is adjusted to the given rectangle.
The following variations of the display are currently supported:
- Bool parameter
"keep_proportion"controls whether to maintain the aspect ratio (default) or not. Rectangle parameter
"clip"restricts the visible part of the source page rectangle. Default is the full page.
- Bool parameter
float
"rotation"rotates the display by an arbitrary angle (degrees). If the angle is not an integer multiple of 90, only 2 of the 4 corners may be positioned on the target border if also"keep_proportion"is true.Bool parameter
"overlay"controls whether to put the image on top (foreground, default) of current page content or not (background).
Use cases include (but are not limited to) the following:
“Stamp” a series of pages of the current document with the same image, like a company logo or a watermark.
Combine arbitrary input pages into one output page to support “booklet” or double-sided printing (known as “4-up”, “n-up”).
Split up (large) input pages into several arbitrary pieces. This is also called “posterization”, because you e.g. can split an A4 page horizontally and vertically, print the 4 pieces enlarged to separate A4 pages, and end up with an A2 version of your original page.
Technical Implementation#
This is done using PDF “Form XObjects”, see section 8.10 on page 217 of Adobe PDF References. On execution of a Page.show_pdf_page(), the following things happen:
The
resourcesandcontentsobjects of source page in source document are copied over to the target document, jointly creating a new Form XObject with the following properties. The PDFxrefnumber of this object is returned by the method.
/BBoxequals/Mediaboxof the source page
/Matrixequals the identity matrix.
/Resourcesequals that of the source page. This involves a “deep-copy” of hierarchically nested other objects (including fonts, images, etc.). The complexity involved here is covered by MuPDF’s grafting [1] technique functions.This is a stream object type, and its stream is an exact copy of the combined data of the source page’s
contentsobjects.This Form XObject is only executed once per shown source page. Subsequent displays of the same source page will skip this step and only create “pointer” Form XObjects (done in next step) to this object.
A second Form XObject is then created which the target page uses to invoke the display. This object has the following properties:
/BBoxequals the/CropBoxof the source page (or"clip").
/Matrixrepresents the mapping of/BBoxto the target rectangle.
/XObjectreferences the previous Form XObject via the fixed namefullpage.The stream of this object contains exactly one fixed statement:
/fullpage Do.If the method’s
"oc"argument is given, its value is assigned to this Form XObject as/OC.The
resourcesandcontentsobjects of the target page are now modified as follows.
Add an entry to the
/XObjectdictionary of/Resourceswith the namefzFrm(with n chosen such that this entry is unique on the page).Depending on
"overlay", prepend or append a new object to the page’s/Contentsarray, containing the statementq /fzFrm<n> Do Q.
This design approach ensures that:
The (potentially large) source page is only copied once to the target PDF. Only small “pointer” Form XObjects objects are created per each target page to show the source page.
Each referring target page can have its own
"oc"parameter to control the source page’s visibility individually.
Redirecting Error and Warning Messages#
Since MuPDF version 1.16 error and warning messages can be redirected via an official plugin.
PyMuPDF will put error messages to sys.stderr prefixed with the string “mupdf:”. Warnings are internally stored and can be accessed via fitz.TOOLS.mupdf_warnings(). There also is a function to empty this store.
Coordinates#
This is one of the most frequently used terms in this documentation. A coordinate generally means a pair of numbers (x, y) referring to some location, like a corner of a rectangle (Rect), a Point and so forth. The two values usually are floats, but there a objects like images which only allow them to be integers.
To actually find a coordinate’s location, we also need to know the reference point for x and y - in other words, we must know where location (0, 0) is positioned. Once (0, 0) (the “origin”) is known, we speak of a “coordinate system”.
Several coordinate systems exist in document processing. For instance, the coordinate systems of a PDF page and the image created from it are different. We therefore need ways to transform coordinates from one system to another (and also back occasionally). This is the task of a Matrix. It is a mathematical function which works much like a factor that can be “multiplied” with a point or rectangle to give us the corresponding point / rectangle in another coordinate system. The inverse of a transformation matrix can be used to revert the transformation. Much like multiplying by some factor, say 3, can be reverted by dividing the result by 3 (or multiplying it with 1/3).
Coordinates and Images#
Images have a coordinate system with integer coordinates. Origin (0, 0) is the top-left point. x values must be in range(width), and y values in range(height). Therefore, y values increase if we go downwards. For every image, there is only a finite number of coordinates, namely width * height. A location in an image is also called a “pixel”.
How large an image will be (in centimeters or inches) when e.g. printed, depends on additional information: the “resolution”. This is measured in DPI (dots per inch, or pixels per inch). To find the printed size of some image, we therefore must divide its width and its height by the corresponding DPI values (there may separate ones for width and for height) and will get the respective number of inches.
Origin Point, Point Size and Y-Axis#
In PDF, the origin (0, 0) of a page is located at its bottom-left point. In MuPDF, the origin (0, 0) of a page is located at its top-left point.
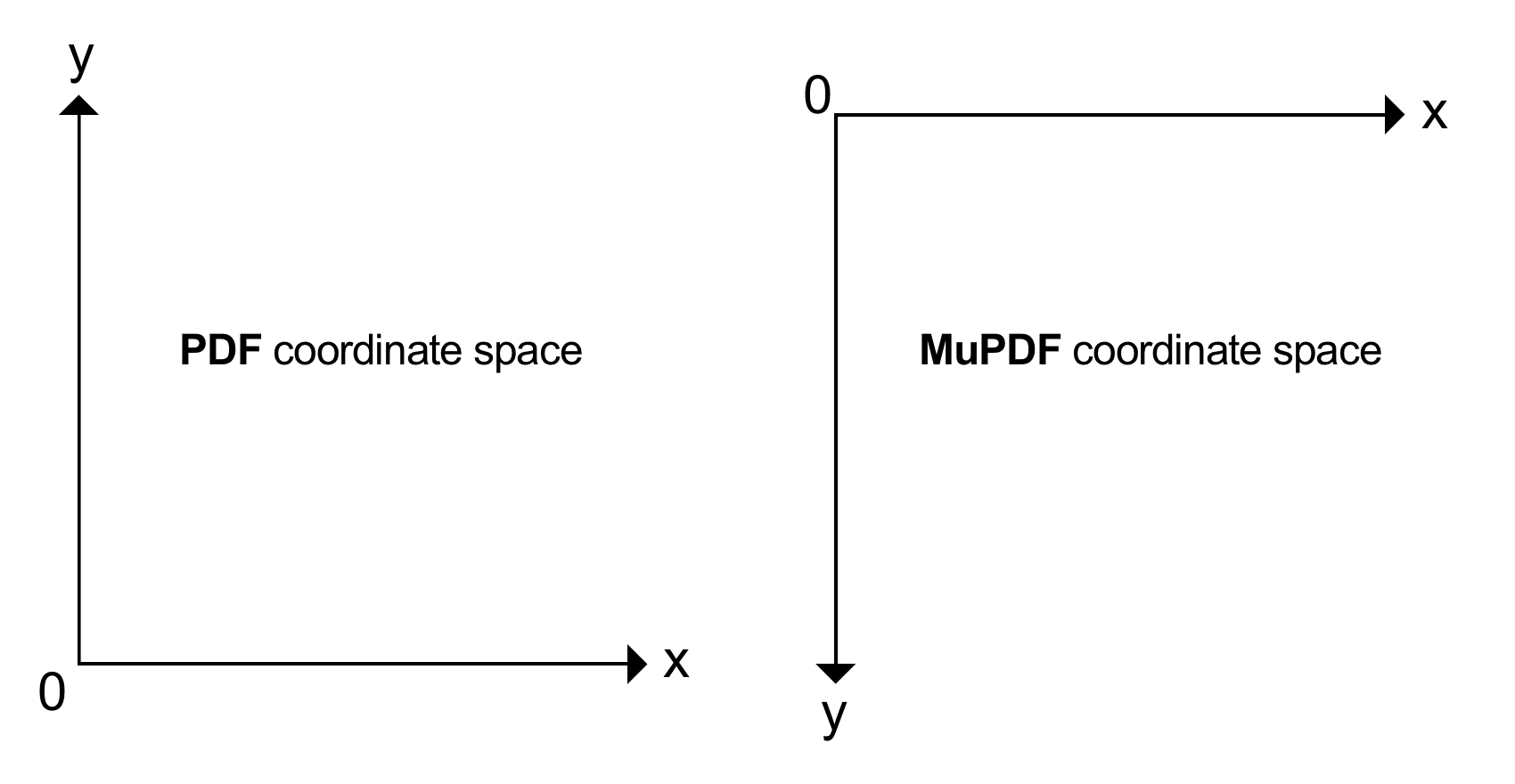
Coordinates are float numbers and measured in points, where:
one point equals 1/72 inches.
Typical document page sizes are ISO A4 and Letter. A Letter page has a size of 8.5 x 11 inches, corresponding to 612 x 792 points. In the PDF coordinate system, the top-left point of a Letter page hence has the coordinate (0, 792) as the y-axis points upwards. Now we know our document size the MuPDF coordinate system for the bottom right would be coordinate (612, 792) (and for PDF this coordinate would then be (612,0)).
Theoretically, there are infinitely many coordinate positions on a PDF page. In practice however, at most the first 5 decimal places are sufficient for a reasonable precision.
In MuPDF, multiple document formats are supported - PDF just being one among over a dozen others. Images are also supported as documents in MuPDF (therefore having one page usually). This is one of the reasons why MuPDF uses a coordinate system with the origin
(0, 0)being the top-left point of any document page. The y-axis points downwards, like with images. Coordinates in MuPDF in any case are floats, like in PDF.A rectangle
Rect(0, 0, 100, 100)for instance in MuPDF (and thus PyMuPDF) therefore is a square with edges of length 100 points (= 1.39 inches or 3.53 centimeters). Its top-left corner is the origin. To switch between the two coordinate systems PDF to MuPDF, every Page object has aPage.transformation_matrix. Its inverse can be used to compute a rectangle’s PDF coordinates. In this way we can conveniently find thatRect(0, 0, 100, 100)in MuPDF is the same asRect(0, 692, 100, 792)in PDF. See this code snippet:>>> page = doc.new_page(width=612, height=792) # make new Letter page >>> ptm = page.transformation_matrix >>> # the inverse matrix of ptm is ~ptm >>> fitz.Rect(0, 0, 100, 100) * ~ptm Rect(0.0, 692.0, 100.0, 792.0)
Footnotes